Contents:
The Local Likelihood Sampling Algorithm
The Local Importance Sampling Algorithm
The LS-N-IPS Algorithm
Sequential Importance Sampling with Higher Order Dynamical Models
The Local Likelihood Sampling Algorithm
Background : In tracking -at each time step- one usually has two objects that
helps calculating the posterior density of the object's pose: the
observation and the density of the object's pose at the previous
time step (prior density). These, with the help of the observation
and dynamical model, give the bases of the observation and the
prediction density. The product of these two densities is
proportional the posterior. This is why the way densities are
represented and the product of them calculated is a key question in
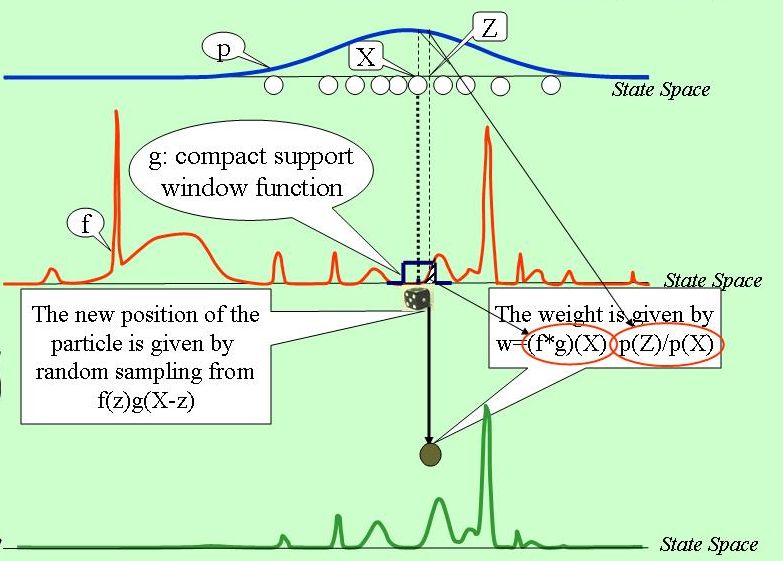
tracking algorithm design. The local likelihood algorithm provides an efficient way of calculating product densities, when one of them is narrowly peaked while the other is broad. These conditions often met in visual object tracking, because the observation density is hoped to be discriminative, while the prediction density is broad to be able to track unexpected movements. The algorithm looks as follows:
The algorithm first draws samples from the prediction density. In the second step, the samples are `moved' towards the modes
of the observation likelihood function, but stay in the close vicinity of the drawn samples thanks
to the compact support of the window function g. Hence the name of the procedure. In
the next step, weights are calculated so that the particle set gives an unbiased estimation of the posterior.
Results
Here
is an MPEG (0.7Mb) showing the
Local Likelihood Sampling algorithm tracking Japanese License Plates.
The tracking works at 65 fps. Only 100 particles were used.
Publications
-
Enhancing Particle Filters using Local Likelihood Sampling
-
Peter Torma and Csaba Szepesvári.
ECCV 2004, Prague. In LNCS Proc.. pp.:16-28
The Local Importance Sampling Algorithm
Background : The Local Importance Sampling algorithm is a generalization of the Local Likelihood sampling algorithm. Will be described in detail in the near future.
The LS-N-IPS Algorithm
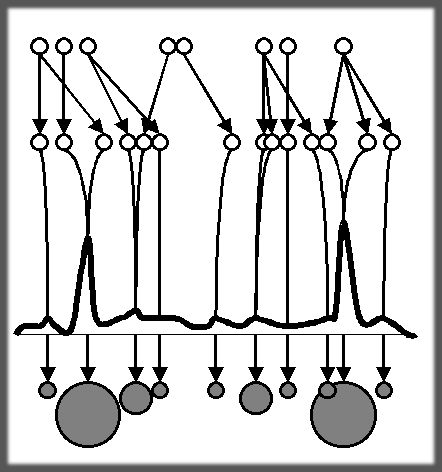
Background : The incremental change between consecutive image frames is always a great help when considering vision based object tracking problems. There are two main approaches in the field that exploit this redundancy. One of them uses the assumption that the object does not move much from frame to frame and employs a local search around the previous object position to locate the object on the next frame. Algorithms in this group tend to be very precise when locked on the object but may have problems if the environment is highly cluttered. The other approach makes use of some filtering algorithm (e.g. Kalman Filter), or particle filtering methods e.g the CONDENSATION algorithm (also called as NIPS in the signal processing literature). The particle filters keep multiple hypothesis about the object state and this increases its robustness against clutter. However, particle filters often give very crude position information unless an excessively large number of particles is used.
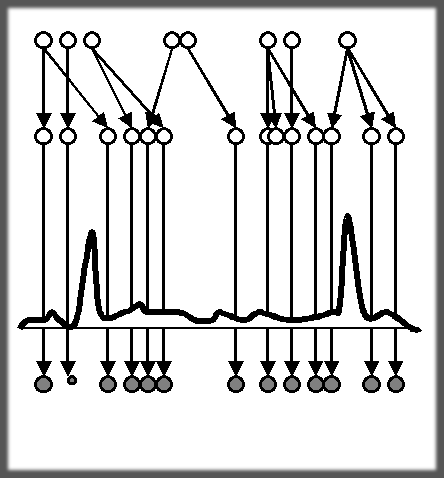
N-IPS, suffers from inefficiency problems if the observation density is uninformative and/or uniformly very small except in a small neighborhood of the true state since then particles which are not in this small vicinity of the ``true'' state will all have roughly equal observation likelihoods and the filter becomes effectively decoupled from the observations.
LS-N-IPS was designed to overcome the problem of N-IPS with peaky observation densities, therefore it is natural to consider it in visual tracking problems. LS-N-IPS combines local search with particle filtering and thus can be thought of as a combination of the two main streams of vision based tracking research mentioned above. As a consequence, the algorithm inherits the high precision of local search based object tracking methods and the robustness of the particle filter based methods, even when a small number of particles is used.
Results
Here is an MPEG (0.7Mb) showing the
LS-N-IPS algorithm tracking an object,
in a cluttered room. The tracking is real time. Only 100 particles were used.
Here is an MPEG (0.5Mb) showing LS-N-IPS algorithm real-time tracking an hand,
in a dark room with 100 particles.
Here is an MPEG (0.7Mb) showing LS-N-IPS algorithm tracking a face,
in a dark room with 100 particles. Real time performance.
This MPEG (0.9Mb) shows tracking a hand moving in front of the face,
in a cluttered room with only 50 particles. 73 frames can be processed in each seconds. The Local Search is done by an artificial neural network trained in advance.
This MPEG (5.8Mb) shows tracking a facial mask moving in 3D. The Local Search here is a local pose from shading algorithm. The left of the image is the original video, while the right hand side is the tracking result.
Publications
-
LS-N-IPS: An Improvement of Particle Filters by means of Local Search
-
Peter Torma and Csaba Szepesvári
Non-linear Control Systems NOLCOS2000, 2000 St Petersburg, Russia
-
Efficient Object Tracking in Video Sequences by means of LS-N-IPS
-
Peter Torma and Csaba Szepesvári
In Proc. ISAP'01 Pula, Croatia, 2001, pages 277-282
-
Towards Facial Pose Tracking
-
Peter Torma and Csaba Szepesvári
In Proc. First Hungarian Computer Graphics and Geometry Conference Budapest, Hungary, 2002, pages 10-16
Sequential Importance Sampling with Higher Order Dynamical Models
Background :We consider sequential importance sampling for filtering dynamical
systems observed in noise and when the importance function is
defined over a few selected components of the state space,
typically the components corresponding to the innovation part of
the process to be filtered. In this case the basic importance
sampling algorithm yields high variance estimates of the
posterior. The problem appears for example in visual tracking
using particle filters when one uses an importance function based
on the output of color blob detector. We proposed
several new methods that are proven to be unbiased and show their
increased efficiency.
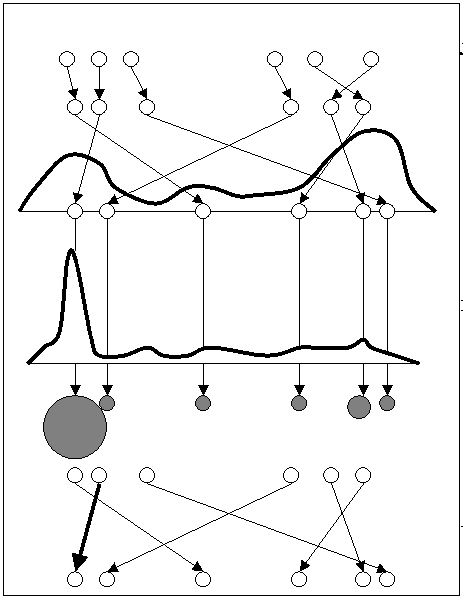
The Basic Sequential Importance Sampling
algorithm can be very inefficient, and may require a large number
of particles to achieve even a modest precision, as many
weights can get small quickly. This is because the importance weight can be very small when
the new state does not match the history. Since the new state is
sampled independently of the past of the process, it can be
"contradicting" with the history of the process.
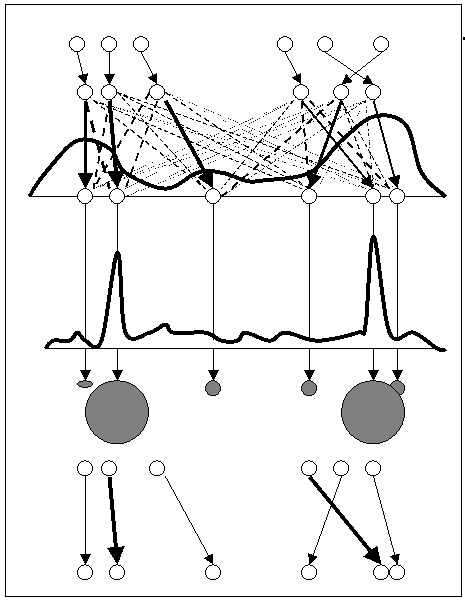
The idea of the algorithms we consider is to ensure that for each
particle the history part of the particle will match the
innovation component sampled from the proposal. Effectively, we
solve this by drawing an appropriate history for each innovation
sampled.
The advantage of the algorithm against the basic SIR algorithm
should be clear: the algorithm selects (by random sampling) pairs
of innovations and histories that have high probability of
co-occurring, by reducing the variance of estimates.
| | | | 
